Limieten Bewijzen

Berekenen

\[f(x)=\frac{x^{2}-5x+6}{x-2}\] Als je hier \(f(2)\) wil benaderen kom je op een deling door 0 uit, dus gebruiken we limieten: \[\lim_{x\to 2}\left(\frac{x^{2}-5x+6}{x-2}\right)\] Dit kunnen we herschrijven als: \[\lim_{h\to 0}\left(\frac{(2+h)^{2}-5(2+h)+6}{(2+h)-2}\right)\] \[\lim_{h\to 0}\left(\frac{4+4h+h^2-10-5h+6}{2+h-2}\right) \] \[\lim_{h\to 0}\left(\frac{h^2-h}{h}\right) \] \[\lim_{h\to 0}\left(\frac{h-1}{1}\right) \] Nu kunnen we invullen. \[\frac{0-1}{1}=-1 \] (In dit geval kan je ook ontbinden in factoren, en dan zie je dan er een factor \(x-2\) weggestreept kan worden, maar de techniek hierboven werkt in het algemeen.)

\(\varepsilon\)-\(\delta\) Definitie.

De limiet bestaat als er voor elke \(\varepsilon>0\) een interval \((a-\delta,a+\delta)\) (met \(\delta>0\) en \(x \neq a\)) te vinden is waarvoor elke \(x\) in dit interval geld: \(|f(x)-l|<\varepsilon\). (\(l=\lim_{x \to a}f(x)\)). Oftewel: Voor elke \(\varepsilon>0\) is er een \(\delta>0\) zodat, als \(0<|x-a|<\delta\), dan is \(|f(x)-l|<\varepsilon\). Om een limiet te bewijzen moet er dus bewezen worden dat als \(0<|x-a|<\delta\) dan volgt daaruit dat \(|f(x)-l|<\varepsilon\).

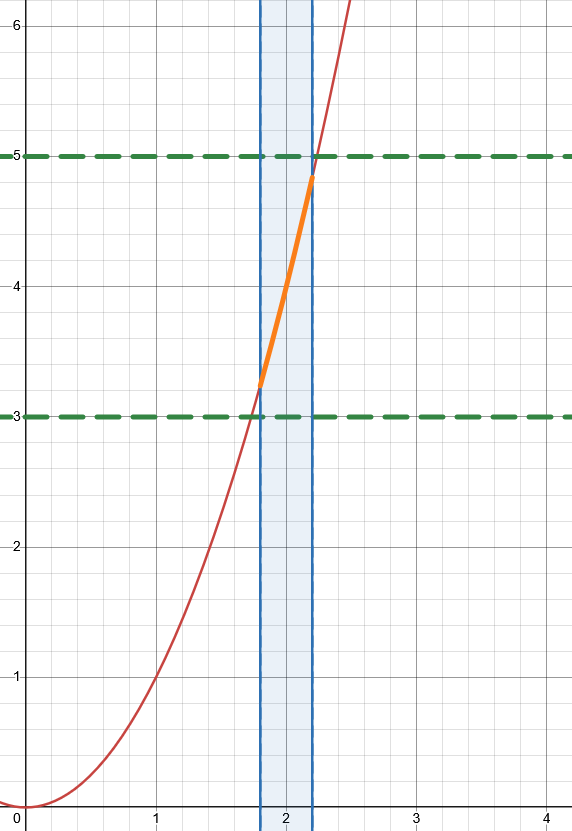
Zie figuur 1. Op figuur 1 is de limiet van \(x^2\) met \(a=2\), \(\varepsilon = 1\) en \(\delta=0.2\) te zien. Het oranje gedeelte is \(f(x)\) op de interval \((a-\delta,a+\delta)\). Het oranje gedeelte komt niet buiten de groene lijnen. Als een \(\delta \neq 0\) bepaald kan worden voor elke waarde van \(\varepsilon\), zodat het oranje gedeelte niet buiten de groene lijnen komt, dan bestaat de limiet op \(a\).

Als we de limiet \(\lim_{x\to 5}(x-3)=2\) willen bewijzen, dan willen we dus bewijzen dat als \(0<|x-5|<\delta\) is daaruit dat \(|(x-3)-2|<\varepsilon\). In feite zoeken we een verband tussen \(\delta\) en \(\varepsilon\) zodat de vorige stelling klopt. \[0<|x-5|<\delta\Rightarrow 0<|x-5|<\varepsilon\] Het is makkelijk te zien dat \(\delta=\varepsilon\) hier werkt: \[0<|x-5|<\varepsilon\Rightarrow 0<|x-5|<\varepsilon\] We kunnen hetzelfde proberen bij de limiet \(\lim_{x \to 3}(x^2)=9\). We willen een verband tussen \(\varepsilon\) en \(\delta\) vinden zodat als \(0<|x-3|<\delta\) is dan is \(|x^2-9|<\varepsilon\). We herschijven eerst op de volgende manier: \[|x-3||x+3|<\varepsilon\] Als we in plaats van een \(|x+3|\) term een constante term hadden, dan zouden we het op deze manier kunnen bewijzen: \[0<|x-3|<\delta \Rightarrow 5|x-3|<\varepsilon\] \[0<|x-3|<\delta \Rightarrow |x-3|<\frac{\varepsilon}{5}\] \[\delta=\frac{\varepsilon}{5}\] Daarom begrenzen we tijdelijk \(\delta\): \[\delta \leq 1\] \[0<|x-3|< 1 \] \[3< |x| < 4\] Dit betekent dat \(|x+3|\) maximaal \(7\) is. Nu kunnen we zien dat als \(\delta \leq 1\) dan is \(\delta\): \[7|x-3|<\varepsilon\] \[|x-3|<\frac{\varepsilon}{7}\] \[0<|x-3|<\delta\] \[\delta=\frac{\varepsilon}{7}\] Deze delta werkt dus voor \(\varepsilon \leq 7\). Dat betekent dat als \(\varepsilon > 7\) een \(\delta\) van \(1\) nog steeds zal werken dus kunnen we nu stellen: \[\delta=\min(1,\frac{\varepsilon}{7})\]

Een belangrijke limiet

We kunnen nu één van de belangrijkste limieten in differentiaalrekening bewijzen: \[\lim_{x \to 0}\left(\frac{\sin(x)}{x}\right)=1\] Om te beginnen stellen we dat: \[0<|x|<\delta\] en \[|\frac{\sin(x)}{x}-1|<\varepsilon\] We gebruiken de Taylor reeks van \(\sin(x)\): \[|\sin{x}|< |x-\frac{x^{3}}{6}| \] \[|\sin{x}-x|< |\frac{x^{3}}{6}| \] Delen door \(|x|\) \[|\frac{\sin{x}}{x}-1|< |\frac{x^{2}}{6}| \] Als \(|\frac{x^{2}}{6}|\) minder is dan \(\varepsilon\), dan is \(|\frac{\sin{x}}{x}-1|\) dat automatisch ook dus stellen we: \[|\frac{x^{2}}{6}|<\varepsilon\] \[|x|<\sqrt{6\varepsilon}\] \[0<|x|<\delta\]

Bewijzen van limiet regels.

Scalaire factor regel

Éen van de regels die men gebruikt bij het berekenen van limieten is \[\lim_{x\to a}cf(x)=cl\] Deze kunnen we als volgt bewijzen als we er vanuit gaan dat we de limiet \(\lim_{x\to a}f(x)=l\) kunnen bewijzen: Gegeven is dat voor elke \(\varepsilon>0\) is er een \(\delta>0\) zodat \(0<|x-a|<\delta \Rightarrow |f(x)-l|<\varepsilon\). In plaats van \(|f(x)-l|<\varepsilon\) kunnen we net zo goed stellen: \(|f(x)-l|<\frac{\varepsilon}{|c|}\) sinds de stelling moet werken voor elke \(\varepsilon\). (We gaan er vanuit dat \(|c| \neq 0\), hier komen we later op terug.) \[0<|x-a|<\delta \Rightarrow |f(x)-l|<\frac{\varepsilon}{|c|}\] Vermenigvuldig met \(|c|\): \[0<|x-a|<\delta \Rightarrow |cf(x)-cl|<\varepsilon\] In het geval dat \(c=0\) moeten we bewijzen dat: \[\lim_{x\to a}0=0\] Dus dat: \[0<|x-a|<\delta \Rightarrow |cf(x)-cl|<\varepsilon\] \[0<|x-a|<\delta \Rightarrow 0<\varepsilon\] Dit klopt altijd, sinds \(\varepsilon>0\).

Somregel

\[\lim_{x\to a}(f(x)+g(x))=l+m\] Dus moeten we bewijzen dat: \[0<|x-a|<\delta \Rightarrow |f(x)+g(x)-l-m|<\varepsilon\] Begin met de twee limieten apart: \[\lim_{x\to a}(f(x))=l\] \[\lim_{x\to a}(g(x))=m\] (Weer gaan we er vanuit dat beide limieten kloppen.) Nu kijken we naar de \(\varepsilon\)-\(\delta\) definitie van beide limieten: \[0<|x-a|<\delta_1 \Rightarrow |f(x)-l|<\varepsilon_2\] \[0<|x-a|<\delta_2 \Rightarrow |g(x)-m|<\varepsilon_2\] Waarbij \(\varepsilon_2 = \frac{\varepsilon}{2}\). We definieren \(\delta=\min(\delta_1,\delta_2)\) en gebruiken hem voor de twee aparte limieten: \[0<|x-a|<\delta \Rightarrow |f(x)-l|<\varepsilon_2\] \[0<|x-a|<\delta \Rightarrow |g(x)-m|<\varepsilon_2\] Hieruit volgt dat \[|f(x)-l|+|g(x)-m|< 2\varepsilon_2=\varepsilon\] Volgens de driehoeksongelijkheid geldt: \[|f(x)-l+g(x)-m| \leq |f(x)-l|+|g(x)-m|\] Waaruit volgt dat: \[|f(x)-l+g(x)-m| \leq |f(x)-l|+|g(x)-m| < \varepsilon\] \[0<|x-a|<\delta \Rightarrow |f(x)+g(x)-l-m| < \varepsilon\]